Tabellenkalkulationsprogramme
Allgemeines
Unter einer Tabellenkalkulation versteht man eine Software die eine interaktive Eingabe und Verarbeitung von numerischen bzw. alphanumerischen Daten in Tabellenform ermöglicht. Vielfach erlauben diese Programme eine graphische Darstellung der Ergebnisse in verschiedenen Anzeigeformen.
Wer ein Tabellenkalkulationsprogramm aufruft (hier zB Excel®), sieht zunächst ein großes weißes Blatt voller Kästchen (eine leere Tabelle). Diese Kästchen werden Zellen genannt und das Blatt als Arbeitsblatt bezeichnet. Dieses Arbeitsblatt hat viel Ähnlichkeit mit einem Rechenheft.

Die Arbeitsfläche am Bildschirm ist also in nummerierte Zeilen und alphabetisierte Spalten eingeteilt. Dadurch können die Zellen eindeutig (durch die jeweilige Spalten- und Zeilennummer zB A2) identifiziert werden.

Jede Zelle einer Tabelle kann Konstanten (zB Zahlen, Text) oder Formeln (zB Berechnungsvorschriften, Programmcodes) beginnend mit einem Gleichheitszeichen enthalten. Für die in der Software vorhandenen Formeln stehen zahlreiche Bibliotheksfunktionen zur Verfügung. Die Formeln können zudem Werte aus anderen Zellen durch entsprechende Adressierung benutzen.
Vorteile von Tabellenkalkulation im Unterricht
Tabellenkalkulationsprogramme bieten vielfältige Möglichkeiten für einen modernen Mathematikunterricht. Sie entlasten von Rechenarbeit und ermöglichen somit eine Konzentration auf Kernelemente der Mathematik, die Thematisierung komplexer Anwendungen, experimentelles Arbeiten sowie eine kritische Auseinandersetzung mit unterschiedlichen Lösungswegen. Argumente welche den Einsatz eines Tabellenkalkulationsprogramms im Mathematikunterricht rechtfertigen sind die schnelle Erstellung ansprechender Graphiken oder das Arbeiten mit eindrucksvollen dynamischen Visualisierungen. Gerade deswegen haben sich solche Programme als Standardwerkzeuge im Mathematikunterricht durchgesetzt. Diese Programme stellen also eine Rechenhilfe in vielen Bereichen dar. Führt man Berechnungen damit durch, werden diese in eine Zelle mittels der Tastatur oder über entsprechende Menübefehle eingegeben. Die dazu möglichen oder notwendigen Datenformate sind vorgegeben:
Was leistet ein Tabellenkalkulationsprogramm?
Arbeitet man mit einem Tabellenkalkulationsprogramm stehen folgende Aspekte im Vordergrund:
- Zahlen und Text in ein Arbeitsblatt (eine Tabelle) eingeben

- Formeln und Funktionen eingeben und zur Berechnung verwenden
Untersuche eine
Geradengleichung
durch Variation
der Steigung bzw. des
Ordinatenabstandes!
Steigung k= 0,50
Ordinatenabstand d= 1,00 |
allgemeine Form der Geradengleichung y= 0,5 *x + 1 |
| x | y=f(x) |
| -10 | -4 |
| -9 | -4 |
| -8 | -3 |
| -7 | -3 |
| -6 | -2 |
| -5 | -2 |
| -4 | -1 |
| -3 | -1 |
| -2 | 0 |
| -1 | 0,5 |
| 0 | 1 |
| 1 | 1,5 |
| 2 | 2 |
| 3 | 2,5 |
| 4 | 3 |
| 5 | 3,5 |
| 6 | 4 |
| 7 | 4,5 |
| 8 | 5 |
| 9 | 5,5 |
| 10 | 6 |
|
- Die eingegebenen Zahlen, Daten, Formeln und Funktionen graphisch aufbereiten, indem man Diagramme erstellt

Oder
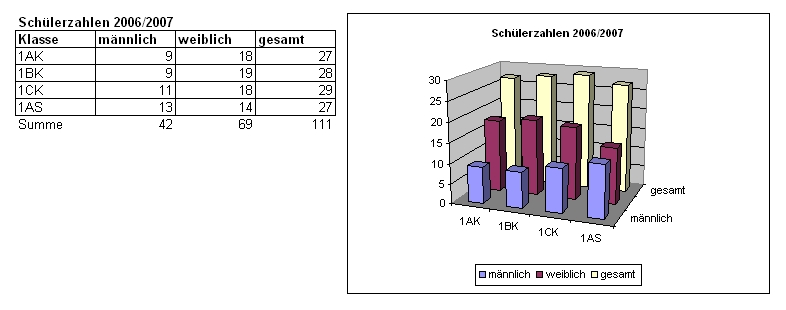
| Erstelle für die gegebenen Schüler(innen)zahlen ein Diagramm und berechne die Summe der jeweiligen Schüler(innen)! Verwende dabei die für die Tabellenkalkulation üblichen Funktionen! |
 |
- Die Darstellung einer Tabelle im Layout verändern und ausdrucken
- Die Eingabe großer Datenmengen automatisieren
Eigenschaften eines Tabellenkalkulationsprogramms
Automatische Neuberechnung
Die Lösung komplexer mathematischer Aufgaben kann mittels einer Tabellenkalkulation meistens nummerisch erfolgen bzw. mittels Simulationen können wertvolle Hinweise zur Lösung einer solchen Aufgabe gefunden werden. Die einfache Erstellung von Graphiken aus berechneten bzw. ausgefüllten Tabellen kann dabei sehr hilfreich sein, insbesondere die sofortige Änderung der Graphiken, bei Änderung der damit in Bezug stehenden Zelleninhalte.
Der entscheidende Vorteil einer Tabellenkalkulation gegenüber einem Rechenheft ist also die Flexibilität. Ändert sich einer der Ausgangswerte, so müssten am Papier alle Berechnungsschritte von neuem durchgeführt werden. Mit einem Tabellenkalkulationsprogramm sind die Formeln bzw. Funktionen in den Zellen verankert, dh. die neuen Ergebnisse werden automatisch neu berechnet.
Mathematische Eingaben
Text wird i.d.R. automatisch als Text erkannt; Zahlen als nummerische Werte, die für Berechnungen verwendet werden können. Man muss jedoch beachten, dass keine Einheiten in Form von Text vorhanden sind dh. Zahlen dürfen nur als reine Zahlen eingegeben werden. In Formeln oder Funktionen ist es notwendig die Eingabe mit dem =-Symbol zu beginnen. Erst dann erkennt das Programm diese als solche. Man kann dann die in der Mathematik gängigen Rechenoperationen einsetzen, welche nach den Regeln der Algebra ausgeführt werden.
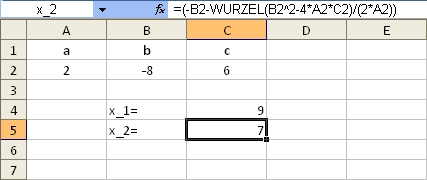
Absolute und relative Adressierung
Um die durchgeführten/geplanten Berechnungen so dynamisch wie möglich zu gestalten sind unterschiedliche Bezugsarten in den jeweiligen Berechnungszellen möglich:
- Relativer Bezug
Eine Anpassung der Zellen beim Kopieren von Formeln oder Funktionen an den Grad der Verschiebung wird als relativer Bezug bezeichnet. Man nennt einen solchen Bezug auch indirekte Adressierung.
- Absoluter Bezug
Möchte man auf eine festgelegte Zelle, weil dort beispielsweise ein Wert angegeben ist, der für alle Berechnungen notwendig ist, verweisen, so ist es vorteilhaft einen absoluten Bezug herzustellen. Dies bezeichnet man auch als direkte Adressierung und wird durch das Setzen eine $-Zeichens durchgeführt. Möchte man eine Spalte fixieren, dann setzt man vor der Spalte das $-Zeichen, zB $A1; möchte man jedoch die Zeile fixieren ist es notwendig das $-Zeichen vor der Zahl zu setzen, zB A$1. Fixiert man eine gesamte Zelle wird vor der Spalte und vor der Zeile das $-Zeichen gesetzt, zB $A$1.
Übersicht über die Adressierungsmöglichkeiten
| Art des Bezugs |
Darstellung am Bildschirm |
nach dem Kopieren |
Relativer Bezug:
sowohl der Spaltenbuchstabe als auch die Zeilennummer sind angepasst | A1 | B2
|
Absoluter Bezug:
durch das Kopieren erfolgt keine Veränderung | $A$1 | $A$1
|
Gemischter Bezug:
relativer Spalten- und absoluter Zeilenbezug | A$1 | B$1
|
| ________________________________________ | |
|
absoluter Spalten- und relativer Zeilenbezug
| $A1 | $A2
|






