Modellierungssoftware
Allgemeines
Mit Hilfe einer Modellierungssoftware (hier zB Dynasys) können Systeme erstellt, analysiert und simuliert werden. Ein solches System besteht aus unterschiedlichen Komponenten verschiedenster Art, die mittels Wirkungsbeziehungen verknüpft sind. Systeme, die ein zeitabhängiges Verhalten aufweisen, also deren Entwicklung nur von der Zeit als unabhängiger Variable abhängen, können als dynamische Systeme bezeichnet werden. Das Systemverhalten erhält man aus dem Zusammenspiel der auftretenden Komponenten.
Vorteile von Modellierungssoftware im Unterricht
Die Software ist ein Werkzeug zur Modellierung und Simulation dynamischer Systeme. Es lassen sich damit Simulationsmodelle mit Hilfe von Modellierungssmethoden der System Dynamics rasch und unkompliziert realisieren. Das Programm Dynasys wurde speziell für schulische Anforderungen, insbesondere im Mathematik- und Physikunterricht, konzipiert und ermöglicht durch eine einfache Handhabung die einfache Umsetzung von Modellen im Unterricht. Dazu trägt im Wesentlichen der graphische Eingabeeditor und die Flussdiagramm-Symbolik sowie eine Beschränkung auf wenige wichtige Grundfunktionen bei. Das erstellte Modell kann nach Eingabe der Anfangswerte
- unter unterschiedlichen Bedingungen erprobt und simuliert werden und
- das jeweilige Verhalten des Modells in Tabellen und Graphen dargestellt werden.
Die Simulationsergebnisse können sowohl als Zeitkurven, Phasendiagramme sowie als Tabellen ausgegeben werden. Zusätzlich besteht die Möglichkeit, dass auch die Modellgleichungen (automatisch) dargestellt werden.
Es lassen sich also Wechselwirkungen in Systemen untersuchen. Das mathematisch exakte Verhalten solcher dynamischer Systeme müsste eigentlich durch Differentialgleichungssysteme beschrieben werden. Diese Gleichungssysteme sind i.d.R. nicht auf einfache Weise (oder vollständig) lösbar. Daher werden sie bei der Modellierung der Systeme im Hintergrund als Differenzen-Gleichungen aufgebaut. In der Simulation werden sie danach schrittweise und approximativ berechnet.
Die charakteristischen Größen
Betrachtet man unterschiedliche Systeme kann man entdecken, dass gänzlich verschiedene Systeme grundsätzlich gleiche Kategorien von Systemelementen enthalten. Das vereinfacht die weiteren Untersuchungen konkreter Systeme. Es können somit die gleichen Bezeichnungen, Symbole, mathematischen Beschreibungen und Computerprogramme verwendet werden, um die Entwicklung solcher dynamischer Systeme zu untersuchen.
Die in einem System auftretenden Komponenten lassen sich im Allg. folgendermaßen für dynamische Systeme unterteilen:
- Parameter / Konstanten
Das sind Größen, die über die Beobachtungszeit immer konstant bleiben. Es handelt sich dabei vor allem um Naturkonstanten, zB die Gravitationsbeschleunigung. Die Darstellung in Dynasys erfolgt folgendermaßen:
 | Parameter |
- Exogene Größen
Das sind veränderliche Größen, die auf das System Einfluss haben, auf die das System selbst aber keinen Einfluss nehmen kann. Die Darstellung in Dynasys erfolgt analog zu den Parametern.
 | exogene Größe |
- Zustandsgrößen (Bestands- bzw. Speichergrößen)
Der jeweilige Zustand dieser Größen kennzeichnet auch den Zustand des Gesamtsystems. Aus diesem Grund sind sie für die Entwicklung des Systems sowie für die Beschreibung und Simulation von großer Bedeutung. Die Darstellung in Dynasys erfolgt folgendermaßen:
 | Zustandsgröße,
Bestandsgröße |
- Anfangswerte (der Zustandsgrößen)
Diese Werte bestimmen die weitere Entwicklung eines Systems entscheidend; daher müssen sie bekannt sein. Sie können in Dynasys durch eine Doppelklick auf das Symbol der Zustandsgrößen als numerischer Wert eingegeben werden.

- Veränderungsraten (der Zustandsgrößen)
Diese Größen bestimmen, ob bzw. wie eine Zustandsgröße zu- bzw. abnimmt. Um die weitere Entwicklung des Systems ermitteln zu können, müssen sie bekannt sein. Die Darstellung in Dynasys erfolgt folgendermaßen:
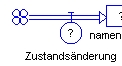 | Zustandsänderung,
Veränderungsrate |
- Zwischengrößen / Funktionen
Dabei handelt es sich um Größen, die sich im Laufe der Zeit verändern, aber ständig aus dem jeweiligen Systemzustand, dh. aus den Zustandsgrößen, ermittelt werden können. Die Darstellung in Dynasys erfolgt folgendermaßen:
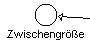 | Zwischengröße |
Modellierungssoftware als Darstellungsmedium
Die Darstellung dynamischer Systeme erfolgt üblicherweise durch sogenannte Wirkungs- und Simulationsdiagramme, also zwei unterschiedliche Arten von Diagrammen um die systemdynamischen Modelle darzustellen.
- Wirkungsdiagramm (Kausaldiagramm)
Dabei handelt es sich um eine erste, noch nicht quantifizierte Darstellung der Wirkungsbeziehung im System. Pfeile zeigen an, wie Systemgrößen auf andere einwirken. Ein Pfeil von A nach B bedeutet: A wirkt auf B.
Durch eine entsprechend gewählte Symbolik, folgend jener der System Dynamics, werden die Veränderungsraten durch Ventile und die Speicherinhalte durch Behälter plastisch dargestellt. Das Funktionieren des Systems wird somit einsichtig. Diese Diagramme eignen sich für eine qualitative Untersuchung im Unterricht.
- Simulationsdiagramm
Hier werden ebenfalls die Wirkungen zwischen den Größen gezeigt. Die Struktur ist die gleiche wie im Wirkungsdiagramm. Doch werden auch unterschiedliche Arten der Größen unterschieden. Die Art der Verknüpfungen zwischen den Systemgrößen wird definiert (wie in den charakteristischen Größen dargestellt):
- Als Symbole werden Kreise bzw. Rechtecke verwendet.
- In roter Farbe sind Parameter bzw. exogene Funktionen der Zeit gekennzeichnet; diese Größen haben keine Eingänge (Eingangspfeile).
- Zwischengrößen sind durch Kreise gekennzeichnet.
- Zustandsgrößen (Bestandsgrößen, Speichergrößen) erscheinen als Rechteck.
Was leistet Modellierungssoftware?
Im Prinzip lässt sich für jede Größe eine Rechenanweisung angeben. Mit Hilfe der Zustandsgrößen werden die neuen Werte aus den alten Werten mittels der Veränderung während eines Zeitschrittes berechnet. Am Beginn entspricht der alte Wert dem vorgegebenen Anfangswert. Alle (Differenzen-)Gleichungen werden von der Modellierungssoftware automatisiert erzeugt.
Dies soll nun anhand von Beispielen dargestellt werden. Für weitere Beispiele wird die Seite von Walter Hupfeld, dem Entwickler dieser Software, empfohlen.
Zunächst betrachten Sie ein bekanntes Beispiel zu Zerfallsprozessen, die sowohl im Mathematik- als auch im Physikunterricht, allenfalls im Chemieunterricht, thematisiert werden. Um zu zeigen, dass damit nicht nur Betrachtungen an einem bestimmten Element durchgeführt werden müssen, ist die gewählte Aufgabenstellung bereits eine Idealisierung der Situation. Gestartet wird für diesen Einstieg bereits im sogenannten Real-Modell.
| Radioaktiver Zerfall | Modellierung in Dynasys |
Betrachte einen radioaktiven Stoff! Der Zerfallsvorgang dieses Stoffes kann durch drei Bedingungen modelliert werden:
- In gleich langen Zeitintervallen verkleinert sich ihre Intensität um den gleichen Faktor.
- Zu Beginn beträgt sie 10000 (in Einheiten, um die wir uns jetzt nicht kümmern wollen).
- Während jeder Stunde halbiert sich ihr Wert.
| Zerfall.dyn |
| mögliche Ausgaben der Software |
| (Differenzen-)Gleichungen |  |
| (Werte-)Tabelle | 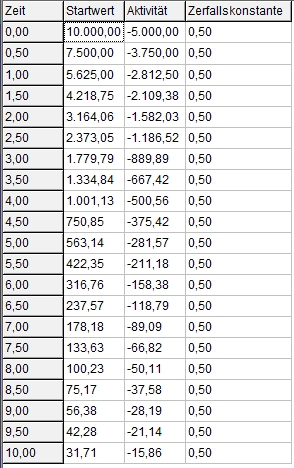 |
| Zeitdiagramm | 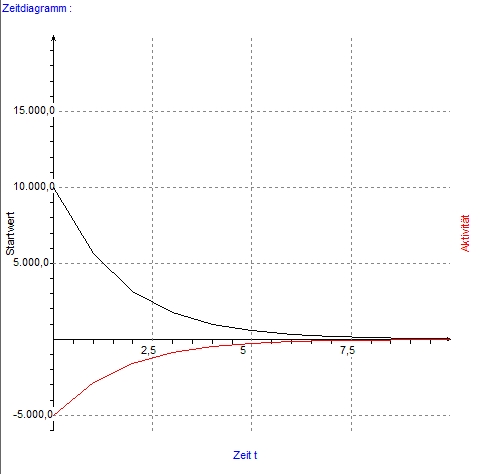 |
Die Komplexität der Modellierung könnte jedenfalls erhöht werden, indem beispielsweise eine Zerfallsreihe betrachtet wird.
| Zerfallskette | Modellierung in Dynasys |
| Angenommen man untersucht einen (radioaktiven) Stoff S1, der in den Stoff S2 zerfällt und dieser in den Stoff S3, welcher dann stabil ist. Zudem hat man bereits ermitteln können, dass in der ersten Stunde 1 % von S1 und 2 % von S2 zerfallen. | Kette.dyn |
| mögliche Ausgabe der Software |
| Differenzen-Gleichung |  |
| Zeitdiagramm | 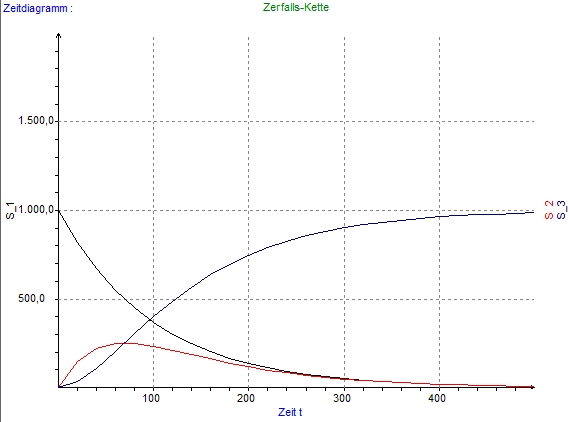 |
Ein weiteres Beispiel, welches in einer anderen Umsetzung auf der Homepage von Hupfeld gefunden werden kann, ist die Modellierung eines Fallschirmsprungs.
| Fallschirmsprung | Modellierung in Dynasys |
| Bei der Modellierung eines Fallschirmsprungs interessieren die Höhe (des Absprungs), die Geschwindigkeit sowie die Beschleunigung des Fallschirmspringers, insbesondere die Grenzgeschwindigkeit beim freien Fall (mit Luftwiderstand) und jedenfalls die Geschwindigkeit bei der Landung. Auch die Kräfte beim Öffnen eines Fallschirms, Einflüsse verschiedener Parameter wie beispielsweise die Größe des Fallschirms oder das Gewicht des Fallschirmspringers können zu interessanten Fragestellungen führen. | Fallschirmsprung.dyn |
| mögliche Ausgaben der Software |
| (Differenzen-) Gleichungen | 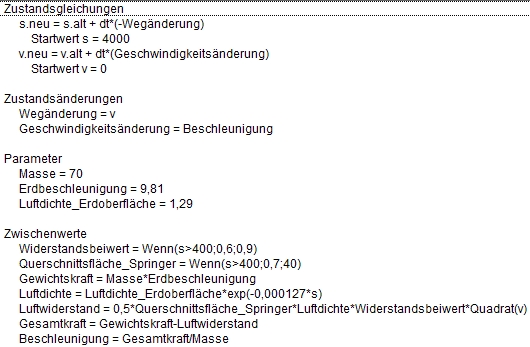 |
| Zeitdiagramm | 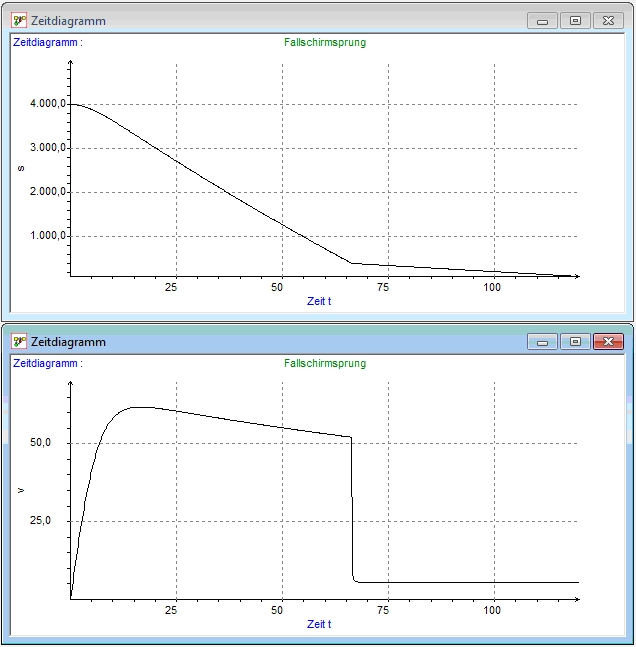 |