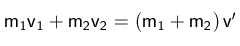
Gegeben sind zwei Körper der Massen m1 und m2, die sich mit den Geschwindigkeiten v1 beziehungsweise v2 auf einer geraden Linie bewegen. Die Geschwindigkeitswerte sind mit Vorzeichen versehen. Bewegung in eine Richtung wird durch ein Pluszeichen ausgedrückt, Bewegung in die entgegengesetzte Richtung durch ein Minuszeichen.
Nach einem vollkommen unelastischen Stoß "kleben" die beteiligten Körper aneinander, sodass sie dieselbe Geschwindigkeit (v') haben. Zur Berechnung von v' benötigt man den Impulserhaltungssatz, nach dem die Summe der Impulse vor und nach dem Stoß gleich sein muss.
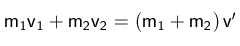
Auflösung dieser Gleichung nach v' ergibt:
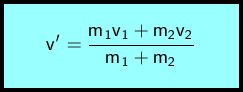
m1 ... Masse des ersten Körpers
v1 ... Geschwindigkeit des ersten Körpers vor dem Stoß (mit Vorzeichen)
m2 ... Masse des zweiten Körpers
v2 ... Geschwindigkeit des zweiten Körpers vor dem Stoß (mit Vorzeichen)
v' ... Geschwindigkeit beider Körper nach dem Stoß
Auch hier gilt der Impulserhaltungssatz, aber die Körper haben nach dem Stoß verschiedene Geschwindigkeiten v1' und v2'.
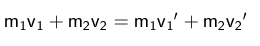
Da zwei Unbekannte zu berechnen sind, benötigt man eine weitere Gleichung. Man erhält diese aus dem Energieerhaltungssatz. Die Summe der kinetischen Energien bleibt beim Stoß konstant; es erfolgt also keine Umwandlung kinetischer Energie in eine andere Energieform.
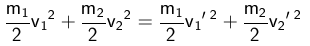
Durch Auflösen der ersten Gleichung nach einer Unbekannten, Einsetzen in die zweite Gleichung und algebraische Umformung erhält man die gesuchten Geschwindigkeiten nach dem Stoß:
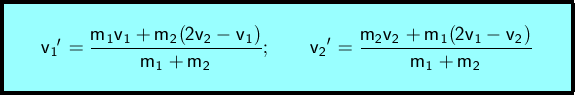
m1 .... Masse des ersten Körpers
v1 .... Geschwindigkeit des ersten Körpers vor dem Stoß (mit Vorzeichen)
v1' ... Geschwindigkeit des ersten Körpers nach dem Stoß (mit Vorzeichen)
m2 .... Masse des zweiten Körpers
v2 .... Geschwindigkeit des zweiten Körpers vor dem Stoß (mit Vorzeichen)
v2' ... Geschwindigkeit des zweiten Körpers nach dem Stoß (mit Vorzeichen)
URL: http://www.walter-fendt.de/ph14d/stossmath.htm
© Walter Fendt, 1. Februar 2010