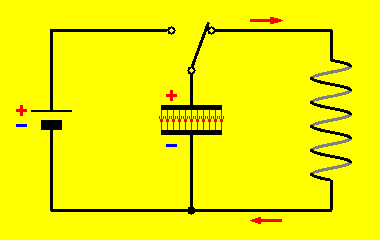
Ein elektromagnetischer Schwingkreis besteht aus einem Kondensator und einer Spule. Der Kondensator ist gekennzeichnet durch die Kapazität C. Die Spule hat die Induktivität L und den ohmschen Widerstand R; im Idealfall der ungedämpften Schwingung gilt

Zunächst sollen die Vorzeichen der elektrischen Größen festgelegt werden. Q sei die Ladung der oberen Platte des Kondensators, U die Spannung zwischen den Kondensatorplatten. Q und U sind positiv, solange die obere Platte positiv und die untere Platte negativ geladen ist. Für die Stromstärke I soll positives Vorzeichen einen Strom im Uhrzeigersinn bedeuten (technische Stromrichtung, von Plus nach Minus!).
Die kirchhoffsche Maschenregel liefert folgenden Ansatz:
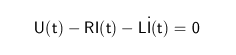
Spannung und Stromstärke sind zeitabhängig und werden deshalb als Funktionen von t beschrieben. Die drei Summanden der Gleichung stehen für die Kondensatorspannung, den Spannungsabfall in der Spule sowie die in der Spule induzierte Spannung. Die Gleichung muss noch so umgeformt werden, dass nur noch eine zeitabhängige elektrische Größe vorkommt, zum Beispiel die Ladung. Die Kondensatorspannung ist der Quotient aus Ladung und Kapazität. Die Stromstärke ist bei der verwendeten Vorzeichenfestlegung gleich der negativen Ableitung der Ladung nach der Zeit. (Zeitliche Ableitungen werden üblicherweise durch Punkte ausgedrückt.)
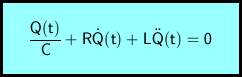
In dieser Gleichung kommen neben der gesuchten Funktion auch Ableitungen dieser Funktion vor. Man spricht von einer Differentialgleichung, genauer von einer linearen Differentialgleichung 2. Ordnung mit konstanten Koeffizienten.
Differentialgleichungen haben im Allgemeinen unendlich viele Lösungen. Eindeutig festgelegt wird die Lösung durch zwei Anfangsbedingungen: Zur Zeit
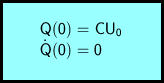
Entsprechend lautet die Differentialgleichung für die Spannung:
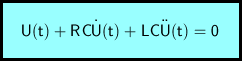
Die zugehörigen Anfangsbedingungen sind:
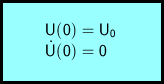
Bei der Lösung dieser Differentialgleichung stellt sich heraus, dass drei Fälle zu unterscheiden sind, nämlich der Schwingfall, der Kriechfall und der aperiodische Grenzfall.
Ist der Widerstand der Spule nicht zu groß, so kommt es zu elektromagnetischen Schwingungen. Die genaue Bedingung lautet:
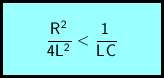
Um die Lösung einfach hinschreiben zu können, führt man zwei Abkürzungen ein.
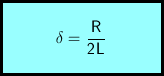
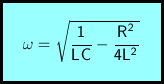
δ wird als Dämpfungsfaktor bezeichnet. ω ist die Kreisfrequenz der Schwingung. Die gesuchte Lösung der Differentialgleichung für die Spannung unter Berücksichtigung der Anfangsbedingungen (partikuläre Lösung) lautet:
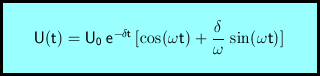
Die Ladung der oberen Kondensatorplatte ergibt sich durch Multiplikation mit der Kapazität.

Die Stromstärke schließlich erhält man durch Differenzieren nach der Zeit und Umkehrung des Vorzeichens.
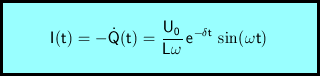
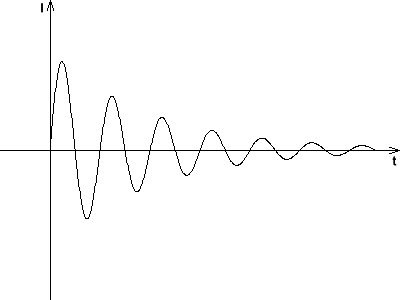
Wesentlich einfachere Rechenausdrücke erhält man, wenn der Widerstand R der Spule den Wert 0 hat. In diesem Fall verschwindet der Dämpfungsfaktor δ.
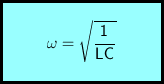
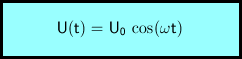
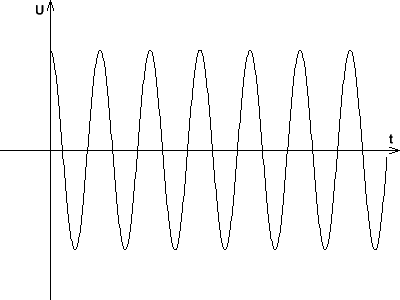
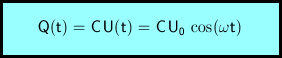
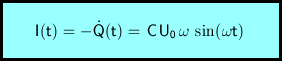
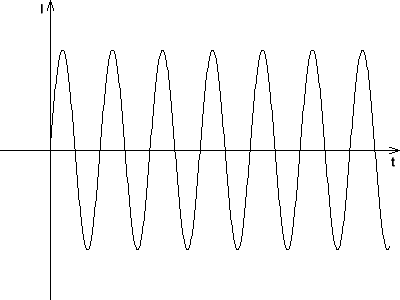
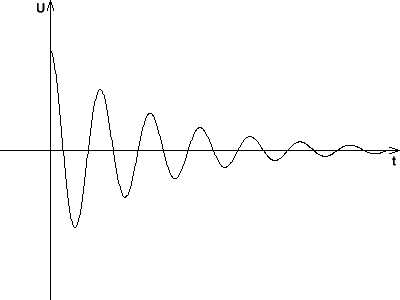
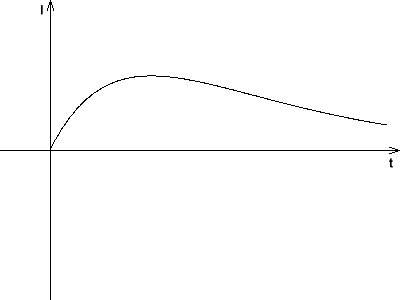
Der Schwingfall ist dadurch gekennzeichnet, dass Spannung, Ladung und Stromstärke periodisch ihre Vorzeichen ändern. Ganz anders verhält sich der Schwingkreis, wenn
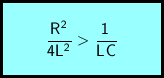
gilt. In diesem Fall haben Spannung, Ladung und Stromstärke immer dasselbe Vorzeichen. Auch hier werden zur einfachen Formulierung der Lösung Abkürzungen verwendet.
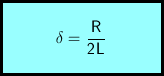
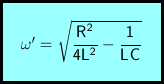
δ ist wie im Schwingfall definiert. Im Rechenausdruck für ω' wurden gegenüber der entsprechenden Definition von ω unter der Quadratwurzel Minuend und Subtrahend vertauscht, da diese Wurzel sonst nicht definiert wäre.
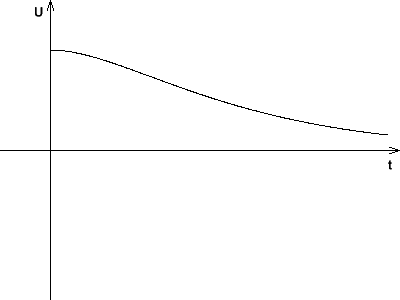
Die Rechenausdrücke für Spannung, Ladung und Stromstärke sind:
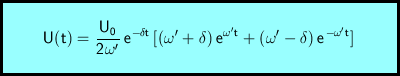
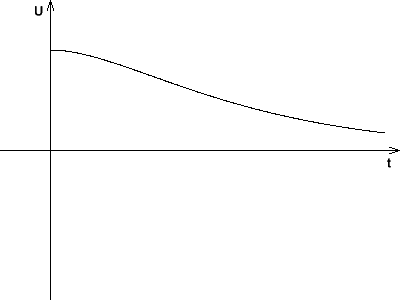
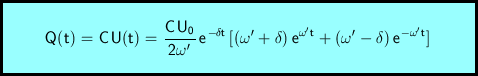

Der aperiodische Grenzfall bildet die Grenze zwischen Schwingfall und Kriechfall. Er tritt auf unter der folgenden Bedingung:
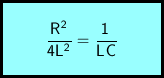
Die Hilfsgröße δ wird in der gleichen Bedeutung wie in den anderen Fällen verwendet.
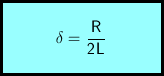
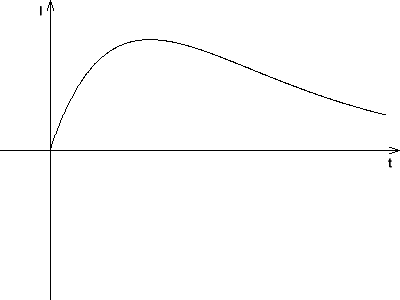
Für Spannung, Ladung und Stromstärke erhält man:
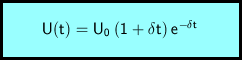
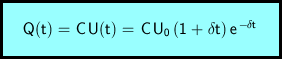
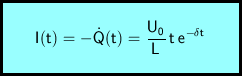
URL: http://www.walter-fendt.de/ph14d/schwingkreismath.htm
© Walter Fendt, 8. August 2007
Letzte Änderung: 2. Februar 2010