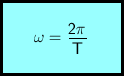
Zur Beschreibung von Kreisbewegungen verwendet man neben der Geschwindigkeit
im üblichen Sinn häufig die Winkelgeschwindigkeit. Diese ist definiert
als Quotient des durchlaufenenen Winkels (im Bogenmaß) und der dafür
benötigten Zeit. Die Zeit für einen Umlauf wird üblicherweise mit T
abgekürzt. Der entsprechende Winkel beträgt im Bogenmaß
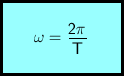
ω ... Winkelgeschwindigkeit
π ... Kreiszahl (3,14159...)
T ... Umlaufdauer
Es wird vorausgesetzt, dass sich ein (im Idealfall punktförmiger) Körper mit gegebener Winkelgeschwindigkeit auf einer Kreisbahn mit gegebenem Radius bewegt. Die momentane Position des Körpers wird durch kartesische Koordinaten ausgedrückt.
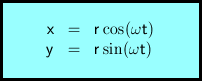
t ... Zeit
x ... erste Koordinate
y ... zweite Koordinate
r ... Radius
ω ... Winkelgeschwindigkeit
Die Geschwindigkeitskomponenten erhält man durch Differenzieren bezüglich der Zeit t (Kettenregel beachten!). vx und vy bilden zusammen den Geschwindigkeitsvektor, der tangential zur Kreisbahn gerichtet ist.
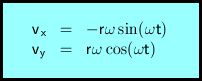
t .... Zeit
vx ... erste Komponente des Geschwindigkeitsvektors
vy ... zweite Komponente des Geschwindigkeitsvektors
r .... Radius
ω .... Winkelgeschwindigkeit
Für den Betrag des Geschwindigkeitsvektors ergibt sich:
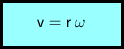
v ... Geschwindigkeit (Betrag des Geschwindigkeitsvektors)
r ... Radius
ω ... Winkelgeschwindigkeit
Erneutes Differenzieren bezüglich t liefert die Komponenten des Beschleunigungsvektors. Dieser ist nach innen, also zum Mittelpunkt der Kreisbewegung gerichtet. Man spricht von der Zentripetalbeschleunigung.
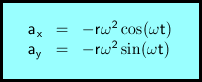
t .... Zeit
ax ... erste Komponente des Beschleunigungsvektors
ay ... zweite Komponente des Beschleunigungsvektors
r .... Radius
ω .... Winkelgeschwindigkeit
Für den Betrag des Beschleunigungsvektors folgt daraus:
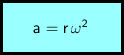
a ... Zentripetalbeschleunigung (Betrag des Beschleunigungsvektors)
r ... Radius
ω ... Winkelgeschwindigkeit
URL: http://www.walter-fendt.de/ph14d/kreisbewegungmath.htm
© Walter Fendt, 4. August 2007
Letzte Änderung: 2. Februar 2010