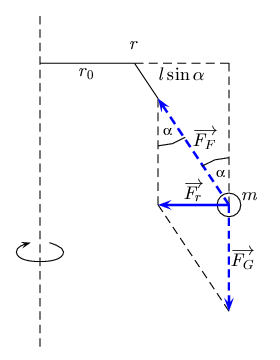
Auf die am Faden hängende Masse m wirken zwei Kräfte, nämlich die Gewichtskraft (nach unten gerichtet) und die vom Faden ausgeübte Zwangskraft (schräg nach oben). Die Gesamtkraft dieser beiden Kräfte (Vektoraddition!) ist die nach innen zur Drehachse gerichtete Zentripetalkraft.

Der Skizze entnimmt man den Ansatz
| tan α = |
| . |
Durch Einsetzen der Formeln für den Betrag der Zentripetalkraft
Fr = m r ω2
und den Betrag der Gewichtskraft
FG = m g
erhält man
| tan α = |
| = |
| . |
Berücksichtigt man außerdem (siehe Zeichnung)
r = r0 + l sin α,
so ergibt sich die Bedingung
tan α = |
| . |
Aus dieser Gleichung lässt sich durch ein Näherungsverfahren (zum Beispiel eine Intervallschachtelung) der Winkel α bestimmen.
α .... Winkel zwischen dem Faden und der Senkrechten
Fr ... Betrag der Zentripetalkraft (Radialkraft)
FG ... Betrag der Gewichtskraft
m .... Masse
r .... Radius der Kreisbewegung
ω .... Winkelgeschwindigkeit
g .... Fallbeschleunigung
r0 ... Abstand der Fadenaufhängung von der Drehachse
l .... Fadenlänge
URL: http://www.walter-fendt.de/ph14d/karussellmath.htm
© Walter Fendt, 12. Dezember 2008
Letzte Änderung: 2. Februar 2010